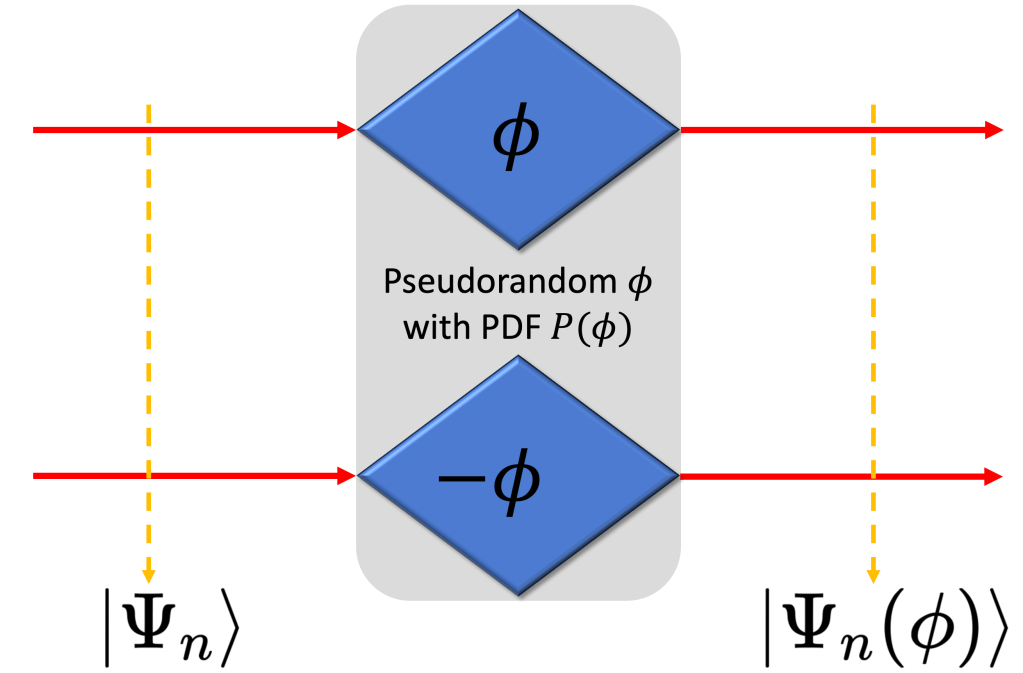
We work on one of the most well-known and important quantum sensing paradigms, that of sensing an optical phase. However, we consider the largely overlooked Bayesian approach. The literature on optical phase sensing in the frequentist approach (i.e., Fisher information approach) is vast, proving retrospectively the importance of said problem. In our work, we examine the case where prior information on the unknown parameter is present in the form of a (prior) probability distribution function (PDF), rendering the unknown parameter a random variable. We take a genuine Bayesian approach: We do not work with Bayesian versions of the Cramér-Rao bound, instead we utilize the so-called minimum mean squared error (MMSE) which is always attainable by a projective measurement.
It is known that the MSE is an improper metric of error for phase sensing when the prior PDF has a large variance. However, in the revised version of our manuscript we focus mainly on small-variance prior PDFs, while our limited (in extent) analysis on large variance priors serves to demonstrate anew the shortcomings of the MSE for said case.
More importantly, starting with small-variance prior PDFs our adaptive technique takes into consideration the updating of the prior PDF, the optimal state and the optimal measurement, per step.
Our work showcases that the robust formalism of the Bayesian MMSE is of high value for phase sensing tasks. Therefore, we are not only delivering new results but at the same time we are giving to the quantum information community the inspiration to work on Bayesian sensing, either by revisiting paradigms and applications well-studied from the Fisherian point of view or by devising genuine Bayesian sensing protocols. This in turn, could lead to a series of further new results which over the years would eventually match in extend and importance their Fisherian counterparts.
For the published version follow this link or click here to read our work on the arXiv.
Quantum information science and technology 